트리
트리 관련 용어

💬 순서 트리와 무순서 트리
◽ 형제 노드의 순서가 있는지 없는지에 따라 트리를 구분할 수 있다.

순서 트리 탐색
너비 우선 탐색
💬 낮은 레벨에서 시작해 왼쪽에서 오른쪽 방향으로 검색하고 한 레벨에서의 검색이 끝나면 다음 레벨로 내려간다.

💬 A -> B -> C -> D -> E -> F -> G -> H -> I -> J -> K -> L
깊이 우선 탐색
💬 리프까지 내려가면서 검색하는 것을 우선순위로 하는 탐색 방법이다.
💬 리프에 도달해 더 이상 검색을 진행할 곳이 없는 경우에는 부모에게 돌아간 후, 순차적으로 자식 노드로 탐색을 이어간다.

전위 순회 (Preorder)
💬 노드 방문 -> 왼쪽 자식 -> 오른쪽 자식
💬 A -> B ->D ->H ->E ->I -> J -> C -> F -> K -> L -> G
중위 순회 (Inorder)
💬 왼쪽 자식 -> 노드 방문 -> 오른쪽 자식
💬 H -> D -> B -> I -> E -> J -> A -> K -> F -> L -> C -> G
후위 순회 (Postorder)
💬 왼쪽 자식 -> 오른쪽 자식 -> 노드 방문
💬 H -> D -> I -> J -> E -> B -> K -> L -> F -> G -> C -> A
이진트리와 이진검색트리
이진트리
💬 노드가 왼쪽 자식과 오른쪽 자식을 갖는 트리를 이진트리라고 한다.

완전이진트리
💬 조건
◽ 마지막 레벨을 제외한 레벨은 노드를 가득 채운다.
◽ 마지막 레벨은 왼쪽부터 오른쪽 방향으로 노드를 채우되 반드시 끝까지 채울 필요는 없다.

💬 따라서, n개의 노드를 저장할 수 있는 완전이진트리의 높이는 logn이다.
이진검색트리
💬 조건
◽ 어떤 노드 N을 기준으로 왼쪽 서브 트리 노드의 모든 키 값은 노드 N의 키 값보다 작아야 한다.
◽ 오른쪽 서브 트리 노드의 키 값은 노드 N의 키 값보다 커야 한다.
◽ 같은 키 값을 갖는 노드는 없다.
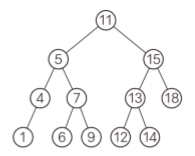
💬 이진검색트리는 중위 순회를 하면 키 값의 오름차순으로 노드를 얻을 수 있으며, 단순하고, 노드의 삽입이 쉽다는 점으로 폭넓게 사용된다.
이진검색트리 만들기
import java.util.Comparator;
public class BinTree<K, V> {
// 노드
static class Node<K, V> {
private K key; // 키 값
private V data; // 데이터
private Node<K, V> left; // 왼쪽 자식 노드
private Node<K, V> right; // 오른쪽 자식 노드
// 생성자
Node(K key, V data, Node<K, V> left, Node<K, V> right) {
this.key = key;
this.data = data;
this.left = left;
this.right = right;
}
// 키 값을 반환
K getKey() {
return key;
}
// 데이터를 반환
V getValue() {
return data;
}
// 데이터를 출력
void print() {
System.out.println(data);
}
}
private Node<K, V> root; // 루트
private Comparator<? super K> comparator = null; // 비교자
...
}
노드 클래스 Node<K, V>
💬 이진트리의 개별 노드를 나타내는 클래스이다.
◽ key : 키 값
◽ data : 데이터
◽ left : 왼쪽 자식 노드에 대한 참조 (왼쪽 포인터)
◽ right : 오른쪽 자식 노드에 대한 참조 (오른쪽 포인터)

이진검색트리 클래스 BinTree<K, V>
◽ root : 루트에 대한 참조를 보존, 유지하는 필드다.
◽ comparator : 키 값의 대소 관계를 비교하는 비교자이다.
생성자
// 생성자
public BinTree() {
root = null;
}
// 생성자
public BinTree(Comparator<? super K> c) {
this();
comparator = c;
}BinTree()
◽ 노드가 하나도 없는 이진검색트리를 생성하는 생성자이다.
◽ 노드 키 값의 대소 관계를 판단할 때 자연 순서에 따라 수행한다.
◽ 비교자를 설정하지 않으므로 필드 comparator 값은 널이 된다.

BinTree(Comparator<? super K> c)
◽ 노드의 대소 관계를 판단할 때 전달받은 비교자에 의해 아래와 같이 수행한다.
◽ this()에 의해 인수를 전달받지 않는 생성자 BinTree()를 호출한다. root가 널인 이진검색 트리를 생성한다.
◽ 필드 comparator에 전달받은 c를 설정한다.
두 키 값을 비교하는 comp 메서드
// 두 키 값을 비교
private int comp(K key1, K key2) {
return (comparator == null) ? ((Comparable<K>)key1).compareTo(key2)
: comparator.compare(key1, key2);
}◽ 이 메서드는 두 키 값 key1과 key2를 비교하여 아래 값을 반환한다.
◽ key1 > key2 -> 양수
◽ key1 < key2 -> 음수
◽ key1 == key 2 -> 0
◽ 비교자 comparator가 null인 경우
((Comparable<K>)key1).compareTo(key2)◽ key1을 Comparable<K> 인터페이스형으로 형변환하고, compareTo 메서드를 호출하여 key2와 비교한다.
◽ 비교자 comparator가 null이 아닌 경우
comparator.compare(key1, key2)
키 값으로 검색하는 search 메서드

💬 알고리즘은 아래와 같다.
◽ 1. 루트부터 선택하여 검색을 진행한다. 여기서 선택하는 노드를 p라고 한다.
◽ 2. p가 널이면 검색에 실패한다.
◽ 3. 검색하는 값 key와 선택한 노드 p의 키 값을 비교하여
◽ 값이 같으면 검색에 성공(검색 종료)합니다.
◽ key가 작으면 선택한 노드에 왼쪽 자식 노드를 대입한다. (왼쪽으로 검색 진행)
◽ key가 크면 선택한 노드에 오른쪽 자식 노드를 대입한다. (오른쪽으로 검색 진행)
◽ 4. 2번 과정으로 돌아간다.
// 키에 의한 검색
public V search(K key) {
Node<K, V> p = root; // 루트에 주목
while (true) {
if (p == null) // 더 이상 진행하지 않으면
return null; // 검색 실패
int cond = comp(key, p.getKey()); // key와 노드 p의 키를 비교
if (cond == 0) // 같으면
return p.getValue(); // 검색 성공
else if (cond < 0) // key 쪽이 작으면
p = p.left; // 왼쪽 서브 트리에서 검색
else // key 쪽이 크면
p = p.right; // 오른쪽 서브 트리에서 검색
}
}
노드를 삽입하는 add 메서드

💬 알고리즘은 아래와 같다.
◽ 1. 루트를 선택한다. 여기서 선택하는 노드를 node로 한다.
◽ 2. 삽입할 키 key와 선택 노드 node의 키 값을 비교한다. 값이 같다면 삽입에 실패한다 (종료).
◽ 값이 같지 않은 경우 key 값이 삽입할 값보다 작으면
◽ 왼쪽 자식 노드가 없는 경우에는 [ a ] 경우와 같이 노드를 삽입한다 (종료).
◽ 왼쪽 자식 노드가 있는 경우에는 선택한 노드를 왼쪽 자식 노드로 옮긴다.
◽ key 값이 삽입할 값보다 크면
◽ 오른쪽 자식 노드가 없는 경우에는 [ b ] 경우와 같이 노드를 삽입한다 (종료).
◽ 오른쪽 자식 노드가 있는 경우에는 선택한 노드를 오른쪽 자식 노드로 옮긴다.
◽ 3. 2번으로 돌아간다.
// node를 루트로 하는 서브 트리에 노드<K, V>를 삽입
private void addNode(Node<K, V> node, K key, V data) {
int cond = comp(key, node.getKey());
if (cond == 0)
return; // key가 이진검색트리에 이미 있음
else if (cond < 0) {
if (node.left == null)
node.left = new Node<K, V>(key, data, null, null);
else
addNode(node.left, key, data); // 왼쪽 서브 트리에 주목
} else {
if (node.right == null)
node.right = new Node<K, V>(key, data, null, null);
else
addNode(node.right, key, data); // 오른쪽 서브 트리에 주목
}
}
// 노드를 삽입
public void add(K key, V data) {
if (root == null)
root = new Node<K, V>(key, data, null, null);
else
addNode(root, key, data);
}
노드를 삭제하는 remove 메서드
💬 자식 노드가 없는 노드를 삭제하는 경우

◽ 삭제할 노드가 부모 노드의 왼쪽 자식이면 부모의 왼쪽 포인터를 null로 한다.
◽ 삭제할 노드가 부모 노드의 오른쪽 자식이면 부모의 오른쪽 포인터를 null로 한다.
💬 자식 노드가 1개인 노드를 삭제하는 경우

◽ 삭제 대상 노드가 부모 노드의 왼쪽 자식이면 부모의 왼쪽 포인터가 삭제 대상 노드의 자식을 가리키도록 한다.
◽ 삭제 대상 노드가 부모 노드의 오른쪽 자식이면 부모의 오른쪽 포인터가 삭제 대상 노드의 자식을 가리키도록 한다.
💬 자식 노드가 2개인 노드를 삭제하는 경우

◽ 1. 삭제할 노드의 왼쪽 서브 트리에서 키 값이 가장 큰 노드를 검색한다.
◽ 2. 검색한 노드를 삭제 위치로 옮긴다 (검색한 노드의 데이터를 삭제 대상 노드 위치로 복사한다).
◽ 3. 옮긴 노드를 삭제한다. 이때
◽ 옮긴 노드에 자식이 없으면 '자식 노드가 없는 노드의 삭제 순서'에 따라 노드를 삭제한다.
◽ 옮긴 노드에 자식이 1개만 있으면 '자식 노드가 1개 있는 노드의 삭제 순서'에 따라 노드를 삭제한다.
// 키 값이 key인 노드를 삭제
public boolean remove(K key) {
Node<K, V> p = root; // 스캔 중인 노드
Node<K, V> parent = null; // 스캔 중인 노드의 부모 노드
boolean isLeftChild = true; // p는 부모의 왼쪽 자식인가?
while (true) {
if (p == null) // 더 이상 진행하지 않으면
return false; // 그 키 값은 없다.
int cond = comp(key, p.getKey()); // key와 노드 p의 키 값을 비교
if (cond == 0) // 같으면
break; // 검색 성공
else {
parent = p; // 가지로 내려가기 전에 부모를 설정
if (cond < 0) { // key 쪽이 작으면
isLeftChild = true; // 왼쪽 자식으로 내려감
p = p.left; // 왼쪽 서브 트리에서 검색
} else { // key 쪽이 크면
isLeftChild = false; // 오른쪽 자식으로 내려감
p = p.right; // 오른쪽 서브 트리에서 검색
}
}
}
if (p.left == null) { // p에는 왼쪽 자식이 없음
if (p == root)
root = p.right;
else if (isLeftChild)
parent.left = p.right; // 부모의 왼쪽 포인터가 오른쪽 자식을 가리킴
else
parent.right = p.right; // Ex) 7을 삭제하는 경우
} else if (p.right == null) { // p에는 오른쪽 자식이 없음
if (p == root)
root = p.left;
else if (isLeftChild)
parent.left = p.left; // Ex) 1을 삭제하는 경우
else
parent.right = p.left; // 부모의 오른쪽 포인터가 왼쪽 자식을 가리킴
} else { // Ex) 5를 삭제하는 경우
parent = p;
Node<K, V> left = p.left; // 서브 트리 가운데 가장 큰 노드
isLeftChild = true;
while (left.right != null) { // 가장 큰 노드 left를 검색
parent = left;
left = left.right;
isLeftChild = false;
}
p.key = left.key;
p.data = left.data;
if (isLeftChild)
parent.left = left.left; // left를 삭제
else
parent.right = left.left; // left를 삭제
}
return ture;
}
모든 노드를 출력하는 print 메서드
💬 모든 노드의 키 값을 오름차순으로 출력하기 위해 중위 순회 방법으로 트리를 검색한다.
// node를 루트로 하는 서브 트리의 노드를 키 값의 오름차순으로 출력
private void printSubTree(Node node) {
if (node != null) {
printSubTree(node.left); // 왼쪽 서브 트리를 키 값의 오름차순으로 출력
System.out.println(node.key + " " + node.data); // node를 출력
printSubTree(node.right); // 오른쪽 서브 트리를 키 값의 오름차순으로 출력
}
}
// 모든 노드를 키 값의 오름차순으로 출력
public void print() {
printSubTree(root);
}
'Data Structure' 카테고리의 다른 글
| 해시 (0) | 2022.01.11 |
|---|---|
| 연결 리스트 (0) | 2021.12.20 |
| 문자열 검색 (0) | 2021.12.14 |
| 배열로 집합 만들기 (0) | 2021.12.13 |
| 재귀 알고리즘 (0) | 2021.11.30 |
